Beschleunigte Systeme - Freien Fall
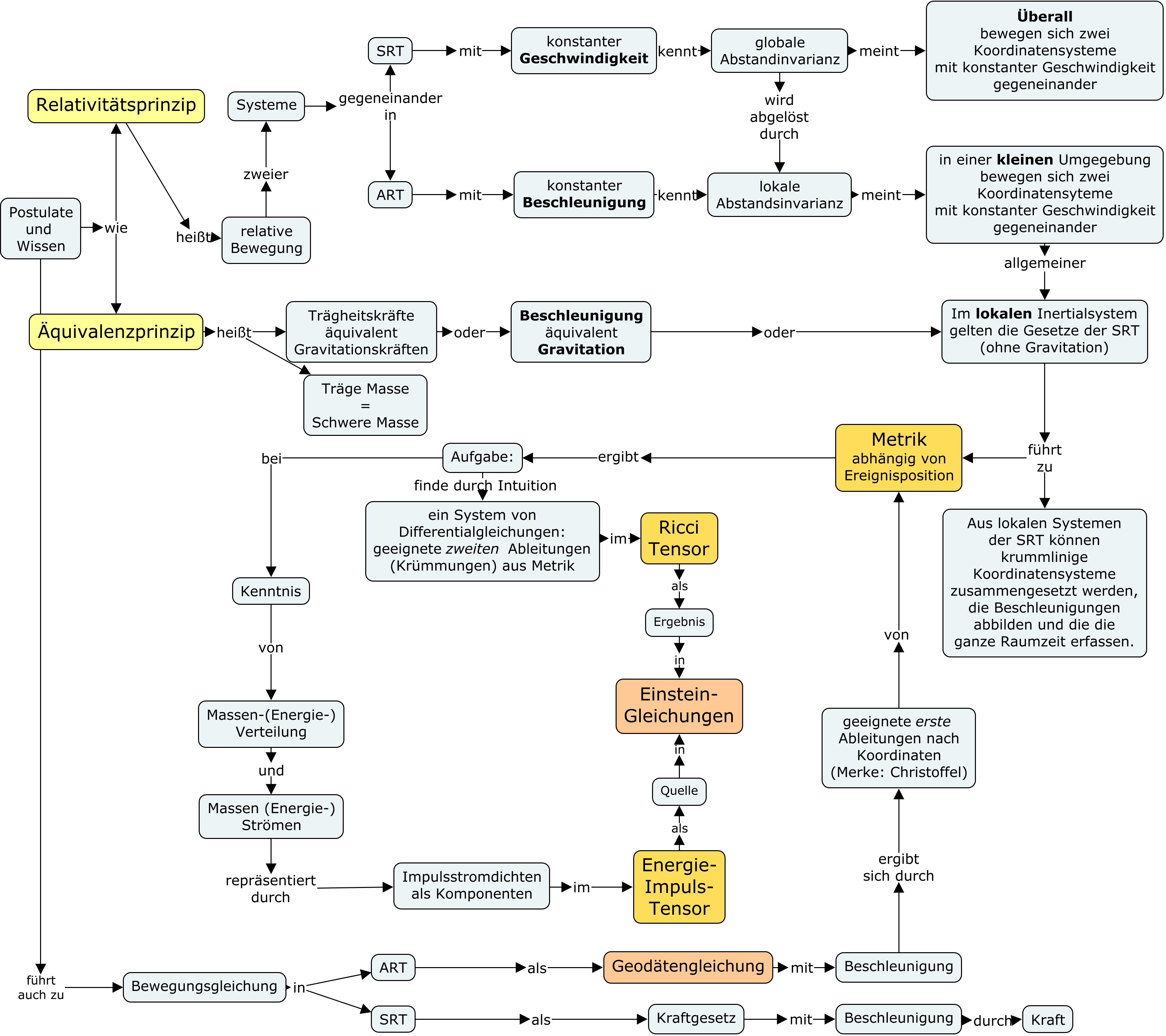
Gegeneinander beschleunigte Systeme sind "gleichberechtigt". Was heißt dieses Prinzip der Relativtät der ART?
Freier Fall und rotierende Bewegung in quasinwetonscher Näherung dienen uns als Anschaungsbeispiele zum Verständnis dieser ersten Grundlage der Allgemeinen Relativitätstheorie.
Beschleunigte Systeme und Gravitation sind äquivalent. Wozu führt das Äquivalenzprinzip?
Längenkontraktion bei einer Kreisbewegung
Die Koordinatensysteme auf Kreisbahnen um einen Mittelpunkt bewegen sich mit unterschiedlichen Geschwindigkeiten zum Bahnmittelpunkt (auch bei konstanter Drehgeschwindigkeit). Das bedeutet, dass für einen Beobachter aus dem Kreismittelpunkt heraus, die Kreisbahnen nicht mehr geschlossen erscheinen. Das tun sie zweifellos nicht. Um die "Lücke", die m it zunehmendem Abstand vom Mittelpunkt größer werden m+üsste, zu schliEs zeigt sich, das die Radiuskoordinate nicht mehr in der Ebene liegen kann und gekrümmt ist.
Änderung der Längen bei Drehbewegung in der Ebene
Für ein kleines Minkowskisystem, das im Mittelpunkt eines Kreises ruht, bewegen sich kleine Minkowskisysteme im Abstand r mit konstanter Geschwindikeit \(\Delta u(r)\).
\(\Delta u = r *\frac {\Delta \phi}{\Delta t}= r * \omega\) mit \(\omega= konstant\)