Konzepte der Relativitätstheorie
In einer Nussschale
Die Konzepte der Speziellen Relativitätstheorie und der Allgemeinen Relativitätstheorie werden hier zusammengefasst und am Beispiel der Zeitdilatation und Längenkontraktion plausibel dargestellt. Gekrümmte Koordinaten sind das Ergebnis der Gleichwertigkeit relativ zueinander bewegter beschleunigter Bezugssysteme. Gravitation ist äquivalent zu Beschleunigung. Gravitation wird erzeugt durch Flüsse von Energie/ Impuls. Das Ergebnis sind gekrümmte Raum-Zeit-Koordinaten.
Allgemeine Relativitätstheorie - Konzept
Bei Anweseheit von Gravitation folgen Zustände, Bewegungen wie Wirkungen (Ereignisse) von massiven und masselosen Objekten (Materie und Licht) den Gesetzen der allgemeinen Relativitätstheorie. Lokal müssen sie den Gesetzen der speziellen Relativtätstheorie gehorchen. Mit "lokal" ist ein (infinitesimal) kleines Raum-Zeit-Gebiet um einen Raum-Zeit-Punkt gemeint. Global spielt sich das Geschehen auf Raum-Zeit-Geodäten ab, deren geometrische Form durch die Verteilung von Energie und Energieströmen (Gravitation) bestimmt ist (aus der speziellen Relativitätstheorie wissen wir, das Masse zu Energie äquivalent ist). Gravitative Energie und gravitativer Impuls können durch Gravitationswellen transportiert werden. Weil die träge gleich der schweren Masse ist, können Beschleunigungen durch irgendwelche Kräfte nicht von Beschleunigungen durch die Schwerkraft unterschieden werden. Einstein folgert daraus, dass physikalische Geetze in gegeneinander beschleunigten Bezugssystemen dieselbe Form haben müssen. Als Konsequenz erfolgen durch Gravitation beschleunigte Bewegungen auf Geodäten des Bezugssystems kräftefrei. Konzepte der Mechanik und der Elektrodynamik werden über den Weg der speziellen Relativitätheorie verallgemeinert und insbesondere Konzepte der Newtonschen Mechanik aufgegeben oder aufgehoben. Das heißt, sie sind im Falle schwacher Gravitation und geringen Geschwindigkeit weiterhin gültig.
More Joomla Extensions
Koordinatensysteme - Spezielle Relativität
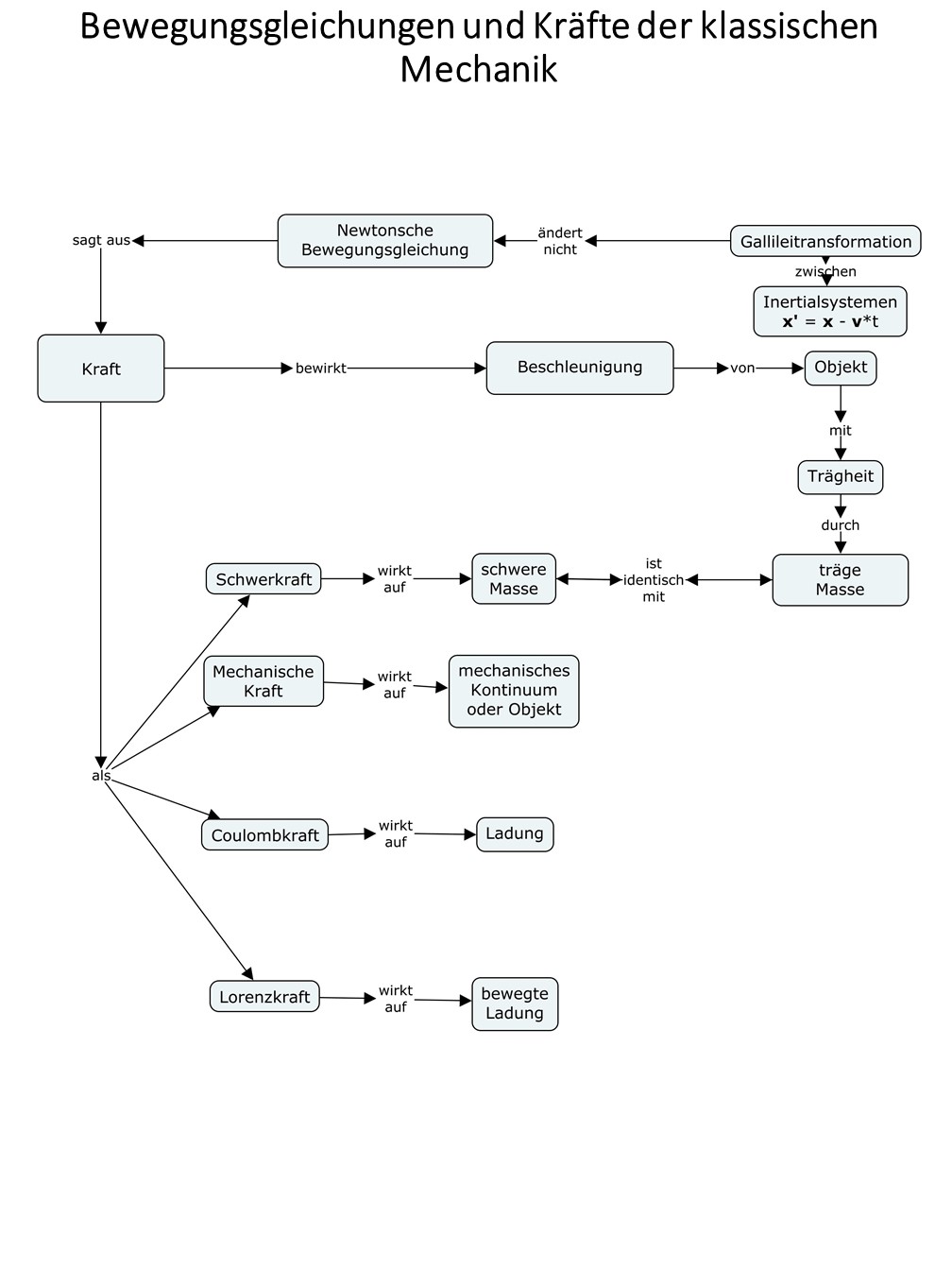
Man kann (mechanische) Bewegungen in verschiedenen Koordinatensytemen beschreiben.
Davon sucht man Inertialsysteme aus. Das sind System, die sich mit konstanter Geschwindikeit gegeneinander bewegen. In all diesen gelten unter Galillei Transformationen die Gesetze der Newtoschen Mechanik bezeihungsweise sie haben dieselbe Form. Diese Transformation scheitert aber an dem experimentellen Ergebnis, dass die Lichtgeschwindigkeit gemessen in allen Inertilasystemen dieselbe ist.
Wenn man Inertialsysteme mit der Lorentz Transformation ineinander überführt, dann gelten die Gesetze der (mechanischen) Spezeillen Relativitätstheorie in allen solchen Systemen beziehungsweise sie haben dieselbe Form. Es gelten auch die Gesetze der Elektrodynamik unter Lorentztransformationen beziehungsweise ihre Formen sind invariant.
Die Lorenztransformation führt zu Ereignissen der Raumzeit, statt der Trennung von Raum (im euklidischen Raum) und einer separaten Zeit. Die Raumzeit wird durch durch den Minkowskiraum beschriegen.
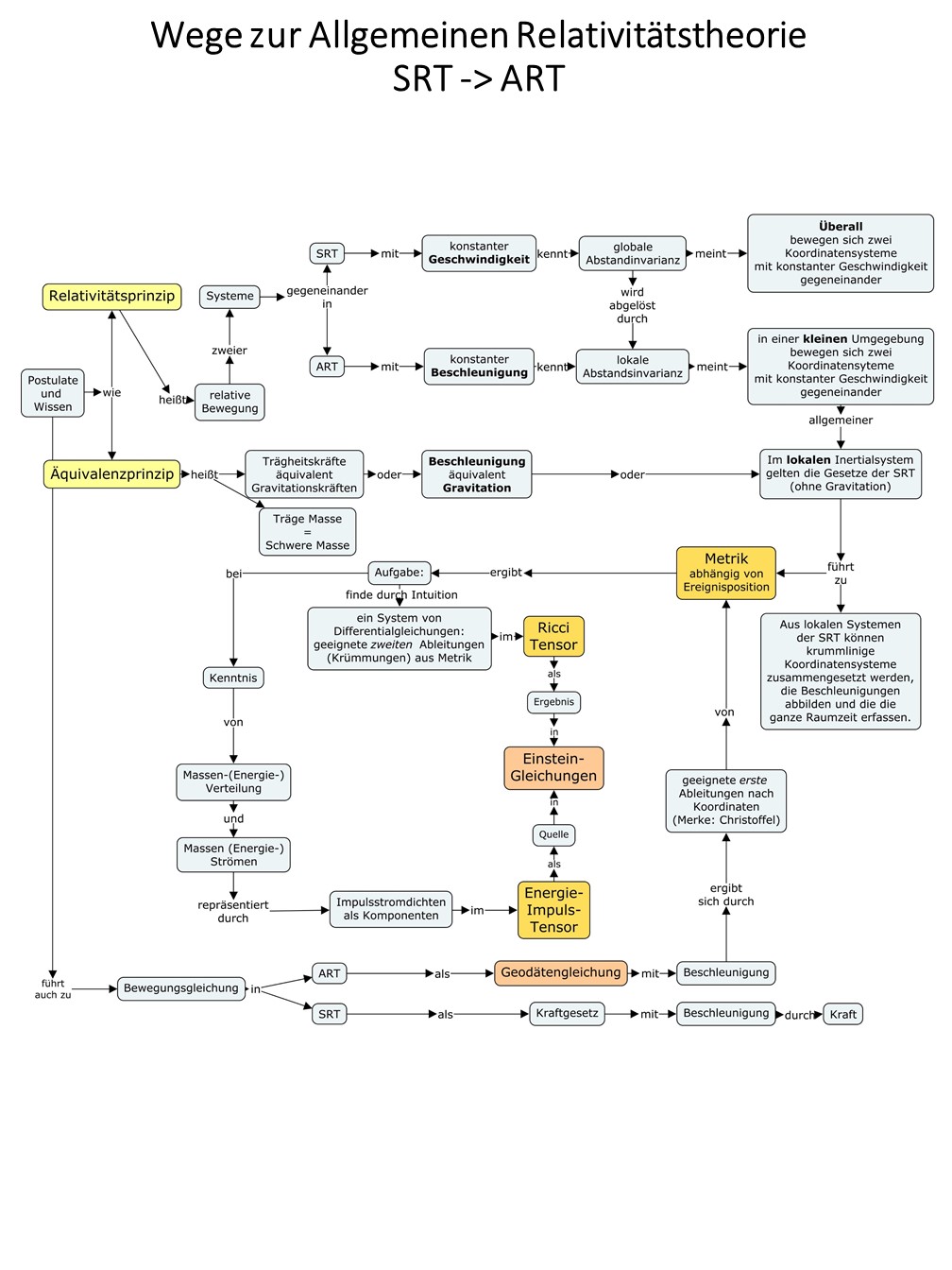
Als Grundlagen der ART gelten das Relativitätsprinzip und das Äquivalenzprinzip. Die Realtivität der speziellen Relativitätstheorie gilt in ganz kleinen Minkowskiräumen. Beschleunigte Bewegung kann man sich durch Raumelemente der SRT zusammengesetzt denken. Äquivalenz von Beschleunigung und Gravitation erklärt die Wirkung der Gravitation. Sie ist die von gegeneinander beschleunigten Bezugssystemen.
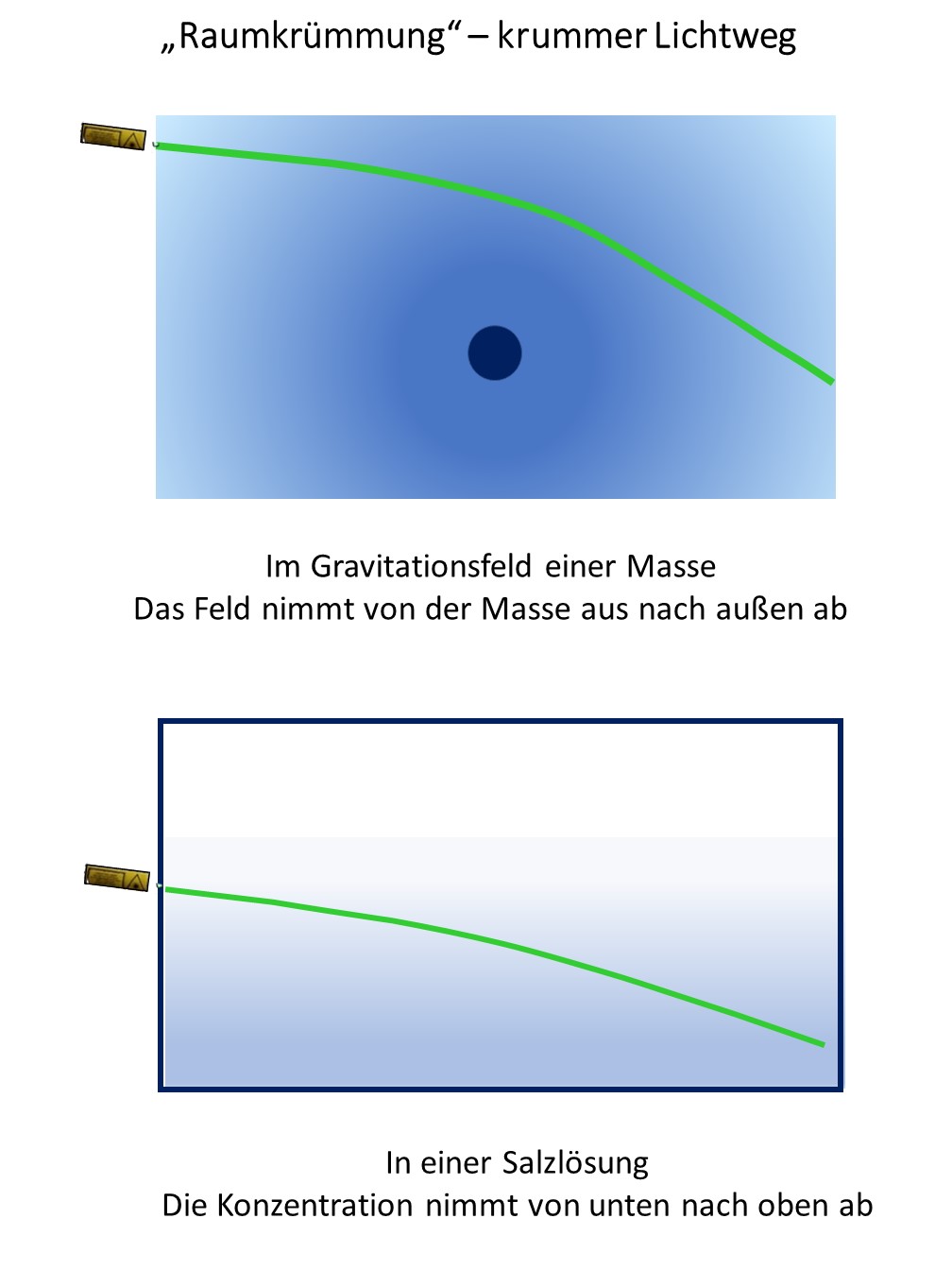
Platt gesprochen führen Zeitdilatation und die Längenkontraktion zur Beschreibung der Graviation durch "krumme" Koordinaten.
Beschleunigte Systeme - Freien Fall
Gegeneinander beschleunigte Systeme sind "gleichberechtigt". Was heißt dieses Prinzip der Relativtät der ART?
Freier Fall und rotierende Bewegung in quasinwetonscher Näherung dienen uns als Anschaungsbeispiele zum Verständnis dieser ersten Grundlage der Allgemeinen Relativitätstheorie.
Beschleunigte Systeme und Gravitation sind äquivalent. Wozu führt das Äquivalenzprinzip?
Längenkontraktion bei einer Kreisbewegung
Die Koordinatensysteme auf Kreisbahnen um einen Mittelpunkt bewegen sich mit unterschiedlichen Geschwindigkeiten zum Bahnmittelpunkt (auch bei konstanter Drehgeschwindigkeit). Das bedeutet, dass für einen Beobachter aus dem Kreismittelpunkt heraus, die Kreisbahnen nicht mehr geschlossen erscheinen. Das tun sie zweifellos nicht. Um die "Lücke", die m it zunehmendem Abstand vom Mittelpunkt größer werden m+üsste, zu schliEs zeigt sich, das die Radiuskoordinate nicht mehr in der Ebene liegen kann und gekrümmt ist.